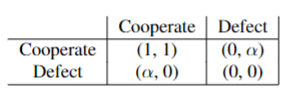
Prisoner Dilemma Simulator
Project attribution: Project done in collaboration with Vlad Pintilie.
Source: The project’s source code is not available.
Short description: Simulator for the Prisoner’s Dilemma experiment.
Technologies: Java, Swing.
What I did: I created the GUI (window, sliders, buttons), the grid and the rules of the experiment. I contributed to the loop of the simulation.
Simulator with GUI for Prisoner’s Dilemma written in Java with the Swing library. Blue patches are cooperating players and red are defecting players. Patches that just switched (in the current iteration) from defection to cooperation are light blue and patches that have switched from cooperation to defection are orange.
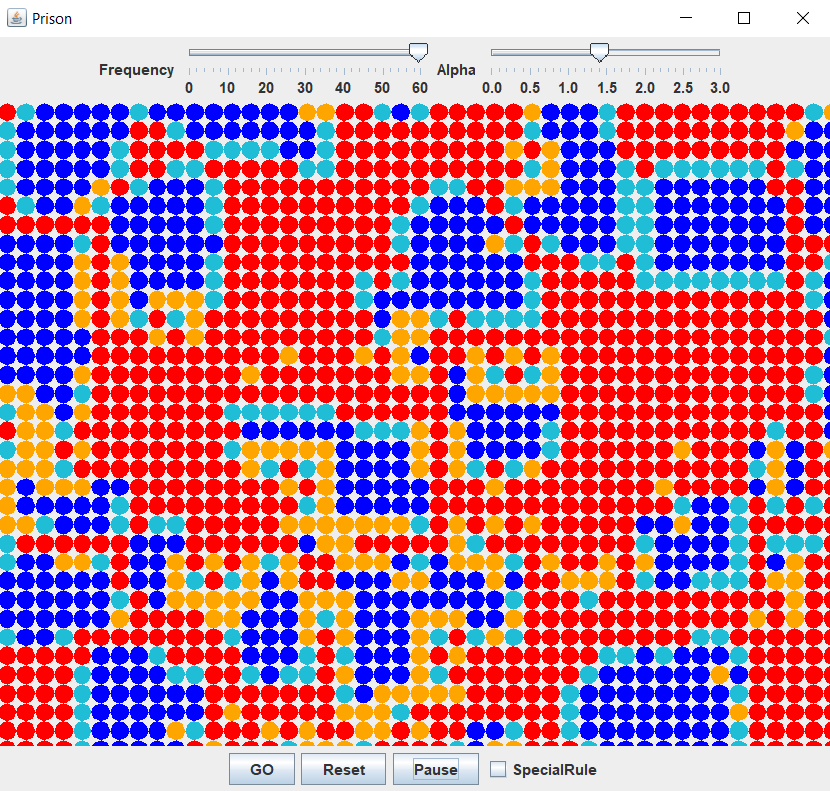
The simulator has a slider for adjusting the frequency of the iterations which implicitly controls the speed of the simulation. A second slider changes the Defection-Award factor (see the Context section). By clicking on a patch, one can change its strategy, i.e. from defection to cooperation and vice-versa. The simulation can be paused and reset (i.e. the game is set in a random position).
Context
One of the most prominently studied phenomena in Game Theory is the Prisoner’s Dilemma. It was formulated by Melvin Drescher and Merrill Flood, and named by Albert W. Tucker. It is an example of a class of games called non-zero-sum games.
In zero-sum games, total benefit to all players add up to zero, or in other words, each player can only benefit at the expense of other players (e.g. chess, football, poker – one person can only win when the opponent loses). On the other hand, in non-zero-games, each person’s benefit does not necessarily come at the expense of someone else.
The simulation runs in cycles. At each cycle, each patch interacts with all of its 8 neighbours to determine the score for the interaction. Should a patch have cooperated, its score will be the number of neighbours that also cooperated. Should a patch defect, then the score for this patch will be the product of the Defection-Award factor α and the number of neighbours that cooperated.